原理请参考《算法导论》
定义一个红黑树类
templateclass rb_tree {public: typedef struct _rb_type { _rb_type(_rb_type *_left, _rb_type *_right, _rb_type *_p, bool cl, T k) : left(_left), right(_right), p(_p), color(cl), key(k) {} bool color;//true for red, false for black T key; _rb_type *left, *right, *p; }rb_type, *prb_type; rb_tree(T *A, int n) :root(NULL) { for (int i = 0; i < n; i++) this->rb_insert(A[i]); } ~rb_tree() { rb_empty(root); } void left_rotate(prb_type x);//左旋 void right_rotate(prb_type x);//右旋 void rb_insert(T key);//插入 prb_type rb_max(prb_type x); prb_type rb_min(prb_type x); prb_type rb_search(T key);//查找 prb_type rb_successor(T key);//后继 prb_type rb_predecussor(T key);//前趋 void rb_delete(T key);//删除 void rb_delete(prb_type z); void rb_empty(prb_type x);//后续全部删除 prb_type Root(); void rb_show(prb_type x);//显示,仅测试使用private: void rb_insert_fixup(prb_type z);//插入后修复 void rb_delete_fixup(prb_type x);//删除后修复 prb_type root;};
相关成员函数的实现
left_rotate成员函数,实现某节点的左旋转
templatevoid rb_tree ::left_rotate(typename rb_tree ::prb_type x) { prb_type y = x->right;//y非空 x->right = y->left; if (y->left) y->left->p = x;//交换子节点 y->p = x->p;//更新父节点 if (x->p == NULL)//将y连接到x的父节点 root = y; else { if (x == x->p->left) x->p->left = y; else x->p->right = y; } y->left = x; x->p = y;}
right_rotate成员函数,实现某节点的右旋转
templatevoid rb_tree ::right_rotate(typename rb_tree ::prb_type x) { prb_type y = x->left; x->left = y->right; if (y->right) y->right->p = x; y->p = x->p; if (x->p == NULL) root = y; else { if (x == x->p->left) x->p->left = y; else x->p->right = y; } y->right = x; x->p = y;}
rb_insert成员函数,将某个key值插入到红黑树中,并修正让其满足红黑树的性质
templatevoid rb_tree ::rb_insert(T key) { prb_type y = NULL, x = root, z = new rb_type(NULL, NULL, NULL, true, key); while (x != NULL) { y = x; if (key < x->key) x = x->left; else x = x->right; } z->p = y; if (y == NULL) root = z; else { if (key < y->key) y->left = z; else y->right = z; } rb_insert_fixup(z);}
rb_insert_fixup成员函数,接上面,根据二叉树插入方法插入后,修正红黑树
templatevoid rb_tree ::rb_insert_fixup(typename rb_tree ::prb_type x) { prb_type y; while (x->p && x->p->color) { //红色 if (x->p == x->p->p->left) { //父节点存在,一定存在祖父节点 y = x->p->p->right; //无法满足性质4 if (!y || y->color) { //若y为NULL,默认不存在的节点是黑色 x->p->color = false; if (y) y->color = false; x->p->p->color = true; x = x->p->p;//重新设置z节点 } else if (x == x->p->right) { //无法满足性质5 x = x->p; left_rotate(x); } if (x->p && x->p->p) { //保证存在 x->p->color = false; x->p->p->color = true; right_rotate(x->p->p); } } else { //和上面左节点相反 y = x->p->p->left; if (!y || y->color) { x->p->color = false; if (y) y->color = false; x->p->p->color = true; x = x->p->p;//重新设置z节点 } else if (x == x->p->left) { x = x->p; right_rotate(x); } if (x->p && x->p->p) { x->p->color = false; x->p->p->color = true; left_rotate(x->p->p); } } } root->color = false;}
rb_search成员函数,根据相关key值,找到对应的节点
templatetypename rb_tree ::prb_type rb_tree ::rb_search(T key) { prb_type x = root; while (x != NULL && key != x->key) { if (key < x->key) x = x->left; else x = x->right; } return x;}
以下几个成员函数,是为了rb_delete函数作准备,分别是rb_max, rb_min, rb_successor, rb_predecessor
rb_max成员函数
templatetypename rb_tree ::prb_type rb_tree ::rb_max(typename rb_tree ::prb_type x) { if (x == NULL) return NULL; while (x->right) x = x->right; return x;}
rb_min成员函数
templatetypename rb_tree ::prb_type rb_tree ::rb_min(typename rb_tree ::prb_type x) { if (x == NULL) return NULL; while (x->left) x = x->left; return x;}
rb_successor成员函数
templatetypename rb_tree ::prb_type rb_tree ::rb_successor(T key) { prb_type x = rb_search(key), y; if (x == NULL) return NULL; if (x->right) return rb_min(x->right); y = x->p; while (y != NULL && y->right == x) { //没有则返回NULL x = y; y = y->p; } return y;}
rb_predecessor成员函数
templatetypename rb_tree ::prb_type rb_tree ::rb_predecussor(T key) { prb_type x = rb_search(key), y; if (x == NULL) return NULL; if (x->left) return rb_max(x->left); y = x->p; while (y != NULL && y->left == x) { x = y; y = y->p; } return y;}
最后,比较关键的删除函数rb_delete成员函数,实现了重载函数,是为了最后测试使用
rb_delete成员函数,重载一
templatevoid rb_tree ::rb_delete(T key) { prb_type z = rb_search(key), y, x; if (z == NULL) return; if (z->left == NULL || z->right == NULL)//y是待删除的节点 y = z;//z有一个子节点 else y = rb_successor(key);//z有两个子节点,后继和前趋保证了y有一个或没有子节点 if (y->left != NULL) x = y->left; else x = y->right; if (x != NULL) //存在一个子节点,先更正父子关系 x->p = y->p; if (y->p == NULL)//再决定是在左或者右节点 root = x; else { if (y->p->left == y) y->p->left = x; else y->p->right = x; } if (y != z)//处理两个子节点的交换 z->key = y->key; if (!y->color)//黑色 rb_delete_fixup(x); delete y;}
重载二
templatevoid rb_tree ::rb_delete(typename rb_tree ::prb_type z) { prb_type y, x; if (z == NULL) return; if (z->left == NULL || z->right == NULL)//y是待删除的节点 y = z;//z有一个子节点 else y = rb_successor(z->key);//z有两个子节点,后继和前趋保证了y有一个或没有子节点 if (y->left != NULL) x = y->left; else x = y->right; if (x != NULL) //存在一个子节点,先更正父子关系 x->p = y->p; if (y->p == NULL)//再决定是在左或者右节点 root = x; else { if (y->p->left == y) y->p->left = x; else y->p->right = x; } if (y != z)//处理两个子节点的交换 z->key = y->key; if (!y->color)//黑色 rb_delete_fixup(x); delete y;}
rb_delete_fixup成员函数,和插入类似,每一次删除一个节点,要调整红黑树颜色让其满足红黑树的性质(原理和rb_insert_fixup相似,不懂实现的,请认真学习《算法导论》)
templatevoid rb_tree ::rb_delete_fixup(typename rb_tree ::prb_type x) { prb_type w; while (x && x!=root && !x->color) { //黑色 if (x == x->p->left) { w = x->p->right; if (w->color) { //红色 w->color = false; x->p->color = true; left_rotate(x->p); w = x->p->right; } if ((!w->left && !w->right)|| (!w->left->color && !w->right->color)) { //双黑 w->color = true; x = x->p; } else { if (!w->right->color) { //单黑 w->left->color = false; w->color = true; right_rotate(w); w = x->p->right; } w->color = x->p->color; x->p->color = false; w->right->color = false; left_rotate(x->p); x = root; } } else { //相反的情况 w = x->p->left; if (w->color) { //红色 w->color = false; x->p->color = true; right_rotate(x->p); w = x->p->left; } if ((!w->left && !w->right) || (!w->left->color && !w->right->color)) { //双黑 w->color = true; x = x->p; } else { if (!w->left->color) { //单黑 w->right->color = false; w->color = true; left_rotate(w); w = x->p->left; } w->color = x->p->color; x->p->color = false; w->left->color = false; right_rotate(x->p); x = root; } } } if (x) x->color = false;//巧妙处理,默认黑}
rb_empty成员函数,按照后续的遍历删除所有的节点
templatevoid rb_tree ::rb_empty(typename rb_tree ::prb_type x) { if (x != NULL) { rb_empty(x->left); rb_empty(x->right); rb_delete(x);//后续保证子叶为空 rb_show(root);//测试使用 printf("-------------------------------------\n"); }}
为了测试所有函数是否正确,定义了一些辅助成员函数(可选)
Root成员函数
templatetypename rb_tree ::prb_type rb_tree ::Root() { return root;}
rb_show成员函数
templatevoid rb_tree ::rb_show(typename rb_tree ::prb_type x) { if (x != NULL) { rb_show(x->left); if (x == root) printf("root: (%s)%d\n", root->color ? "red" : "black", root->key); else printf("(%s)%d\n", x->color ? "red" : "black", x->key); rb_show(x->right); }}
如果要分离模板实现,请提前实例化!!!!
template class rb_tree ;
最后的最后,上测试图吧!
测试一:
数据录入: 11 2 14 1 7 15 5 8 4
如果结果正确,应该生成《算法导论》中的图(如下,深色表示黑色,浅色表示红色)
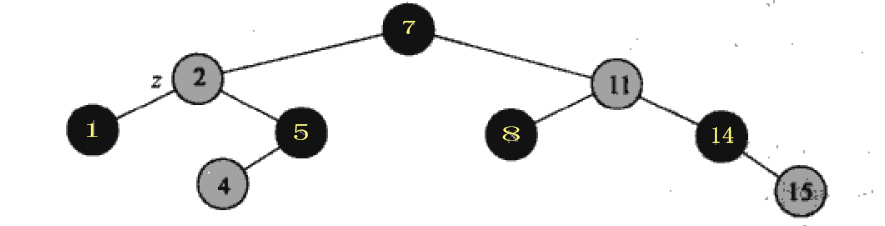
代码产生的结果(正确):

测试二:
录入数据:13 8 17 1 11 15 25 6 22 27
如果结果正确,应该生成以下图的样子
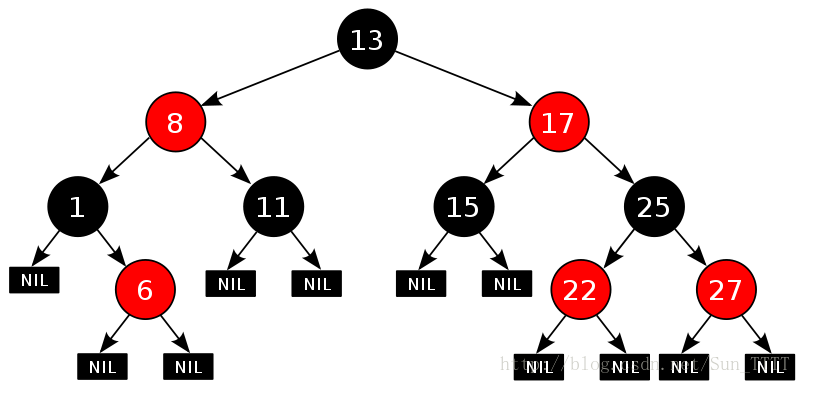
代码产生的结果如下(正确):

测试三:
为了测试所有函数,那么以测试一中的数据为主,然后通过后续逐一删除,并且查看是否删除后,函数能正确的调整红黑树的颜色
未调用删除函数前,完整的红黑树是以下图

然后调用rb_empty成员函数后,产生一下结果(每次删除一个节点,都会显示树的状态和数据,大家花点时间,自己手动删一次,和下面结果一样)

所有代码均经过测试,结果正确!